If a Population Grows 10 Each Year What is the Annual Continuous Growth Rate
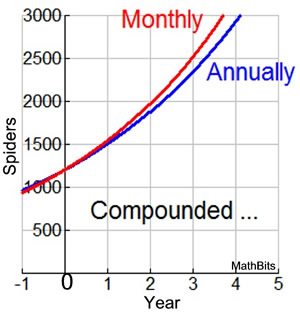
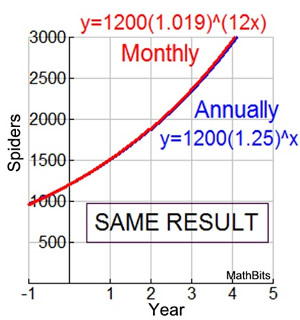
| When working with exponential equations, you may run into a question that wants the resulting equation (or a given equation) re-stated in relation to a different time reference , such as "in months" instead of "in years". Such questions do not want you to change the conditions of the problem. Instead, these questions simply want an equivalent form of the existing equation. EXAMPLE: A study of the annual population of spiders in a certain area shows that the population, P(t), can be modeled by the equation P(t) = 1200(1.25) t , where t represents the number of years since the study began. Write an equation to approximate the population in terms of the monthly rate of growth. Remember the formulas:Increasing: y = a (1 + r) x Decreasing: y = a(1 - r) x Let's start our solution by examining the annual formula, P(t) = 1200(1.25) t = 1200(1 + 0.25) t :
We see from these first three years, that the growth rate is being "compounded " So, what happens if we simply divide the yearly rate of growth (0.25)
By doing this, we are now compounding the growth monthly.
So, how do we get the equation needed for this question? We simply want to write an How can we write the formula with t replaced by 12t, If we simplify the interior of the parentheses, we will have the new monthly rate of growth equation:
Consider the following examples
NOTE: The re-posting of materials (in part or whole) from this site to the Internet is copyright violation | ||||||||||||||||||||||||||||||||||||
Source: https://mathbitsnotebook.com/Algebra2/Exponential/EXTimeRelated.html
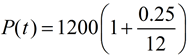
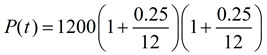
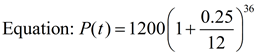
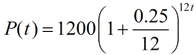
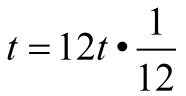
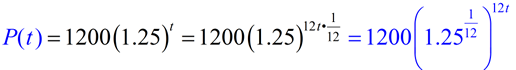
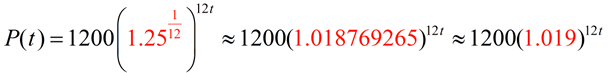
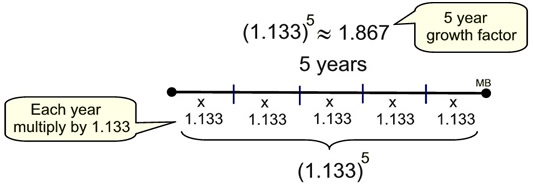
0 Response to "If a Population Grows 10 Each Year What is the Annual Continuous Growth Rate"
Post a Comment